Three Temple Geometry Problems Presented on Beautiful Trees
I am an occasional artist, and have been working for several years on a series of slides now called Japanese Temple Geometry on Beautiful Trees. Geometric diagrams taken from the sangaku are re-created with the GeoGebra program, and placed on photographs of trees (mostly mine) with GIMP (Gnu Image Manipulation Program). This is, of course, an homage to the way that sangaku diagrams were painted on wood. The three problems whose mathematics we will consider are introduced by these slides, in the hope of encouraging a response that transcends the intellectual, perhaps resonating with the aesthetic and spiritual pleasure that the Temple Geometers took in them.
I encourage you to spend some time contemplating the slides before going on to an explanation of the problem and a description of its solution. And also, if you choose to delve into the mathematical side, to return to the slides with the aim of keeping your aesthetic and spiritual appreciation of the problem from being overwhelmed by the intellectual side of the math.
To give a more tangible sense of JTG, we will explore three problems, all from Fukagawa & Rothman’s Chapter 4, Easier Temple Geometry Problems. They are problems with relatively low mathematical complexity that I find beautiful, both visually and conceptually.
They were also chosen to illustrate an interesting tension in the ethos of Temple Geometry. On one hand, there is an intense love of the geometric image, painted in color and hung in a sacred space as an object of contemplation. But on the other hand, there seems to be greater ease with arithmetic and algebraic computations than with creative geometric thinking, and the chosen problems illustrate this.
Problem A. A Surprising Symmetry of Circles (F&R pp 100-101).
The first slide, a shimmering set of sixteen circles, two sets of eight shown twice, gives a sense of what is fixed and what moves in this dynamic problem. Both slides give multiple snapshots of the process, though in very different ways, with the first superimposing two views, and the second giving two separate views, adding a slice of a third. The problem asks the question: Are three circles all the same size? The answer is yes, and it is a surprising symmetry because the construction of the center one is much simpler than that of the outer two. The solution we give was found by the Temple Geometers, and we have not substantially improved on the presentation of Fukagawa & Rothman. It is quite elementary, but it requires drawing some additional lines and using the Pythagorean theorem twice, and then doing some algebra. I have not succeeded in finding a solution that gives a satisfying geometric understanding of the symmetry.
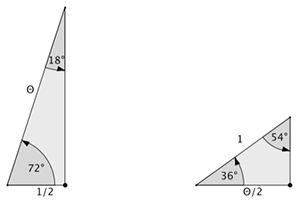
B. The Broken Symmetry of the Pentagram, Problem 33, pp 111-112. This problem is introduced with a single slide of a tree in Regent’s Park 
whose somewhat grotesque beauty seems to invoke the broken symmetry of the pentagram. In contrast to Problem A, the central circle in this case is slightly larger than the circles on the periphery. The problem asks for the size of the break, the ratio of outer to central circles. As we’ll see, the pentagram is thoroughly structured by the Golden Ratio, I wanted to see how θ was used in finding the symmetry-breaking ratio. But the JTG solution given by Fukagawa & Rothman never mentions anything golden, and instead uses some esoteric trigonometry. The solution we give follows F & R, except that the trigonometry is replaced by use of golden triangles. As seen here, there are two golden triangles, isosceles triangles in which the ratio of the longer side to shorter side is always θ. The one on the left is acute, and the one on the right is obtuse.
C. The Elegant Economy of the Susaka Triangle, Problem 47, pp 120-121. Two slides with very different moods introduce this dynamic problem, each superimposing three moments in its growth. One is clear, sharp, reaching dynamically upward. The other, which also contains a diagram of the solution, is murky and mysterious. I love the simplicity of the problem, which contains one right triangle, one circular arc, and one square, and asks a question that has a beautiful answer. The solution of the Temple Geometers was not particularly beautiful. It involved their version of differential calculus. An expression is found for the side of the square in terms of the height of the triangle, and the derivative is set to zero to find the maximum. The answer is agreeably simple, but there is no geometric sense of why it should come out so. F & R present both the JTG proof and a modern proof, which is a model of geometric thinking. Once you really see the diagram, the answer becomes crystal clear. We give an expanded version of the modern proof.
A. A Surprising Symmetry of Circles, Problem 16, pp 100-101.
The left slide contains two snapshots of the dynamic process, which are superimposed. The right slide contains two full snapshots and a slice of a third, but they are distributed. Can you see what the problem might be? Can you separate the two snapshots? Can you see what moves and what stands still?
Problem A
Let’s look at the elements of this problem. There are eight circles in all, but everything is determined by the four red circles of radius r, arranged with their centers in a rectangle. Horizontally, each pair meet in a point, so the rectangle has width 2r, but the vertical dimension, which we call 2t, 
can change. We draw a large red circle around the red circles and a small green circle in the center. Finally we draw two small blue circles between the red and the large green, so that everything touches but doesn’t cross. By symmetry, the left and right blue circles have the same radius q, and we denote the radius of the central circle by p.
The problem asks the question: What is the relationship between p and q? They are very close, but are they actually equal? One might suspect that they are different, since the central green circle only requires the four red circles of radius r, but the two blue circles require that the large red circle be drawn first.
Solution A
The answer is yes, p does equal q. First we add a few lines to the eight circles, forming a triangle with vertices at the centers of three circles: center, upper left, and left, and then divide it into two right triangles by dropping a perpendicular. The hypotenuse of one triangle is r+q and of the other r+p. The proof uses the Pythagorean Theorem twice, once on each of the small right triangles, followed by a bit of algebraic manipulation. Let R denote the radius of the large circle.
Applying the Pythagorean Theorem to the triangle on the right gives:
This demonstration fails to satisfy me. While I can follow the proof and justify every step, it doesn’t answer: Why is the green circle the same size as the blue ones? I have failed to find a geometric argument that gives me a deeper understanding of the geometric construction, which this computation does not do. Nevertheless, I enjoy the problem, and invite you to revisit the two slides now that you have seen the math behind it.
Let me mention one issue that I glossed over above. Once the four red circles are in position, it is easy to locate the center point to draw the small green and large red circles. But it is not obvious how locate the centers of the blue circles, which are tangent to two red circles of radius r, and to the surrounding circle. The problem of constructing a circle tangent to three given circles was not solved by Euclid, but by his great successor Apollonius of Perga, who lived from 262 to 190 BCE. A good reference for his methods is: www.cut-the-knot.org/pythagoras/Apollonius.shtml
Fortunately, in this case we don’t need Appolonius’ method. Once we know that p=q we use the radius of the small green circle to locate the centers of the blue circles.
B. The Broken Symmetry of the Pentagram
The obvious connection between the pentagram and the tree is rotundity, with the tree being an organic explosion of the pristine perfection of the circle, which itself may seem pressed outward by the pentagram and the five circles in its arms. I love the tree for its unruly growth, for breaking the symmetry of a gradually tapering trunk. And the pentagram itself carries a broken symmetry, which is at the heart of this problem. Do you see it?
Problem B
You may have noticed that the green circle in the center appears slightly larger than the five blue circles, which are the same size because of symmetry. That symmetry is broken by the green circle, which is indeed slightly larger. The problem posed on the sangaku is to find out precisely how much larger the central green circle is than the blue circles to find an expression for r, the radius of the green circle, in terms of t, the radius of the blues.
Note that the symmetry that is broken here is rather similar to that which was established in Problem A, as both involve the relationship of a central circle to peripheral ones. When I first considered this problem I was a bit offended. How dare the circles come so close to being equal and yet not actually be the same? Unfair! Then I came to appreciate the broken symmetry, which seems central to placing the figure on this special tree, and is intimately connected with the Golden Ratio.
First, let’s look at the construction of this figure. GeoGebra draws the pentagon automatically, and it is not hard to do it by drawing circles and straight lines, i.e. using ruler and compass. Then the pentagram is an easy construction, as are the small and large green circles. But how do we locate the centers of the five blue circles? That question is answered by the dashed lines at the bottom of the diagram. We extend two of the edges of the pentagram and draw a tangent to the bottom of the circle to form the triangle ΔPXY. Then we can locate the center C of the bottom blue circle by bisecting the angle X and intersecting it with the central line of the pentagram.
Solution B
The answer is that the radius r of the central circle is
This means that the radius of the central circle is about 12% larger than the radii of the blue circles, and the area of the central circle is exactly 25% larger than that of the blues.
If you’re curious about how this answer is obtained, and about the role played by the Golden Ratio and golden triangles, read on. Unlike the JTG proof of the Temple Geometers given by Fukagawa and Rothman, our proof will not use any fancy trigonometry, or any trig at all. The trig is replaced by the golden triangles. First we’ll take a look at how the pentagram is structured by θ. Forget for a moment that you know anything about the Golden Ratio. Everything you need to know about θ can be read off of the pentagram when it’s inscribed in a pentagon, as below:
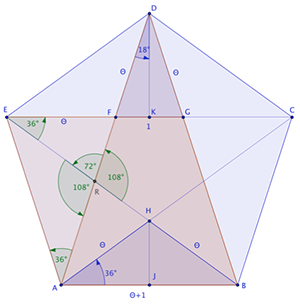Take a good look at this diagram of the pentagram in a pentagon. The angles can all be deduced from the symmetry of the figure.
For simplicity, we set each edge of the inner pentagon to length 1, and now for a moment imagine that θ is not the Golden Ratio, but just the symbol that we happen to use for edges like EF, of which there are 10 (not all labeled). Now notice the parallelogram ABGE, whose top edge has length θ+1, so that the bottom, which is a side of the pentagon, has the same length.
Now notice the triangles ΔFGD and ΔABD. Since they are similar, and the small one is a golden triangle, so is ΔABD, whose long sides are 2θ+1 with short side θ+1. Since
which yields two magic formulas that define the Golden Ratio:
This justifies our use of the symbol θ, and shows that each side of the large pentagon has length θ2=θ+1. We can also find that
which means that the diagonals of the pentagram have length θ3, so every line segment in the figure has length in the set {1, θ, θ2, θ3}. Furthermore, we can now see that every triangle in the pentagram is golden. We now know the angles of the golden triangles.
Because we will encounter them below, we also look at the right triangles obtained by dividing the golden triangles down the middle.
Turning back to the main problem, we start by drawing the diagonal HD, the chord HC and the radius OC, and then drop perpendiculars from P to OC and O to HC. Because it’s one tenth of a full circle, ∠DOC = 36o degrees, and ∠DHC = 18o degrees, half of a pentagram vertex. Notice the two shaded right triangles ΔOWP, which has an angle of 36o degrees and ΔOZH, which has an angle of 18o degrees. Each triangle is half of a golden triangle, so the ratios of corresponding sides will be the same. We let R denote the radius of the large red circle. Then, comparing triangle ΔOZH with the acute half golden triangle gives:
Comparing ΔOWP with the obtuse half golden triangle gives
Using (1) and (2) to eliminate R
Multiplying by θ and using θ2 = θ + 1 gives
which simplifies to
or
Now use
to simplify:
So, if you like your answer in terms of the Golden Ratio:
Since
we have
which puts the difference between r and t in another form:
Congratulations if you hung in to the end of the proof.
For those comfortable with a bit of trigonometry, notice that we have shown these formulas for the angles of golden triangles:
<< Art & Spirit in Mathematics: The Lessons of Japanese Temple Geometry (part I)
Art & Spirit in Mathematics: The Lessons of Japanese Temple Geometry (part III) >>
